fibonacci-number
Fibonacci Number Notations
In mathematics, The Fibonacci numbers are the sequence of numbers defined by the linear recurrence equation \(F_n=F_{n-1} + F_{n-2}\) with \(F_1=F_2=1\).
Semantic
- OpenMath's combinat1/fibonacci
- Fibonacci number in wikipedia
Observations of the symbol
Put your observations here...
English USA 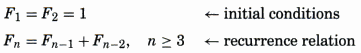
As found in Bibliography, the sequence \(F_n\) of Fibonacci numbers is defined by the recurrence relation. The picture on the right from page num. 269.
Preview google book link
German
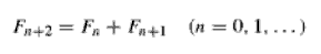 In Bibliography, The recursion for the flog \(F_0, F_1,...\) is the fibonacci-number as shown in the picture on the right from page num. 350.
In Bibliography, The recursion for the flog \(F_0, F_1,...\) is the fibonacci-number as shown in the picture on the right from page num. 350.
See google book link
French 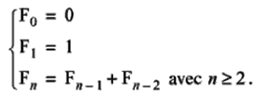
As found in Bibliography, the French book shows the fibonacci-number at the end of page 41.
Preview google book link
Spanish
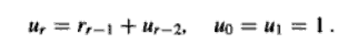 The example on the right shows the fibonacci-number. Find the example in the Spanish book Matematicas para las ciencias aplicadas
The example on the right shows the fibonacci-number. Find the example in the Spanish book Matematicas para las ciencias aplicadas
See google books link